BOWED TONES
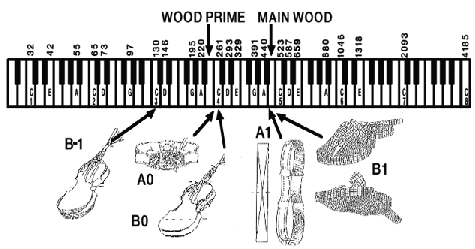
Violin Cavity and Body Modes
It has been shown by means of many tests and actual adjustments to several hundred violin family instruments that certain frequency relationships of the two lowest cavity modes, the A zero (A0) or "Helmholtz" and the A one (A1) body-length mode inside the box, with those of three body modes below 600 Hz can have a marked effect on the tone and playing qualities of an instrument. This writing is an effort to summarize these findings to date and suggest ways in which violin makers can adjust their instruments to take advantage of these frequency relationships. It should be noted that the term PITCH is used for the sound heard, while FREQUENCY is the actual measured Hertz (Hz) of the sound source, and they are not always the same.
Figure 1 shows the geometry and approximate frequencies of these two cavity modes, A0 and A1 and the three body modes, B minus 1 (B-1), B zero (B0) and B one (B1) in a normal violin. Three of these modes, the A0, A1, and B1 are radiating modes, producing sounds out into the air; while the B-1 and the B0 modes are non-radiating, as can be seen from their geometries. Once the violin is completed and strung up it is not advisable to try to move the frequency of the A0 and A1 cavity modes except in a few cases noted below.
BOWED TONES

Violin Cavity and Body Modes
PITCH MATCHING OF A0 AND B0
The best place to begin tuning is to try to bring the B0 mode pitch to that of the A0 mode, for they usually lie fairly close in frequency. Hold the completely strung up violin in thumb and forefinger at a point on the nodal line across the widest part of the lower bout. Damp the strings against your shirt and tap on the end of the scroll. (Do not damp the strings against the fingerboard). The sound heard is the pitch of the B0 mode. Then BLOW across the f-hole on the G-string side (where there is most air motion) and listen to ascertain whether B0 is above or below A0. (These are complex sounds and it is not easy to identify their pitch without practice.)
If the B0 pitch is heard to be HIGHER than the A0, add a small weight, such as a lump of oil clay, or even chewing gum with a penny stuck on it, to the free end of the fingerboard. Notice in the computer visualization of the B0 mode that the end of the fingerboard is moving most actively. (Added mass on a moving element will reduce frequency, as will reduced stiffness in a bending part.) Change the mass slightly until you hear the tapping sound of the B0 mode at the same pitch as the A0 mode BLOW tone. Other ways to lower the B0 mode frequency are to remove wood from under the fingerboard in the area close to the neck, or to thin the bending part of the neck-fingerboard. Dressing down the fingerboard when the strings have worn ridges in it will lower the B0 frequency. The mass of the chin rest as well as that of the scroll and pegs will also alter the B0 frequency. But first try adjusting the mass on the end of the fingerboard and have several good players try the instrument so you can realize the difference. The further apart these two modes are to begin with the more improvement you will get when they are matched.
If the A0 pitch is heard to be HIGHER than the B0, a temporary check can be made by putting various amounts of tape across one f-hole to lower the A0 pitch. Permanent adjustments to do this can be done by reducing the mass of the moving end of the fingerboard either by removing wood from under the end, or sawing thin slivers of wood off the end of the fingerboard until the desired frequency is reached. (Less mass in motion raises frequency.) (See Hutchins 1990a, 1990b, 1990c, 1990d)
It is well known from the early work of Helmholtz that the frequency of a partly enclosed air mass is dependent on the volume of the cavity, the flexibility of its walls, the area of the opening and the thickness of the edges of the opening. The larger and more flexible the cavity, the lower the frequency. The larger the opening and the thinner the edges of the opening, the higher the frequency. Enlargement of the f-hole area has shown experimentally that only a few Hz rise in frequency can be achieved without ruining the f-holes. However thinning and rounding off the underside of the f-hole edges will also cause a slight rise in the A0 frequency since this makes it easier for the air to flow out and in.
A1 AND B1 FREQUENCY RELATIONSHIPS
It has been found that the frequency spacing (delta) between the A1 cavity mode and the B1 body mode is critical to the overall tone and playing qualities, indicating whether a violin is suitable for soloists (delta 60-80 Hz), orchestra players (delta 40-60 Hz), chamber music players (delta 20-40 Hz), and below 20 Hz is easy to play but lacks power (Hutchins 1989). The physical mechanism taking place as a radiating cavity mode and a radiating body mode approach each other in frequency is described in Hutchins and Rodgers 1992.
Violins with fairly stiff free plates (mode #5 at 370 Hz and Mode 2 at 185 Hz) often have their A1-B1 delta around 60-75 Hz and are preferred by soloists for their bright powerful sound and wide dynamic range, while those with lower free plate frequencies (360-180 Hz or 350-175 Hz) are more suitable for some orchestra players and amateurs. (Free plate frequencies do not always produce the desired delta of A1-B1 since other factors such as stiffness of ribs, liners, and edge thicknesses enter in.)
Various methods that have been tried to alter the A1-B1 delta show the following frequency changes of the B1 mode:
| 1. Prolonged vibration vibration | minus 10 Hz |
| 2. Liners thinned 1/2 mm | minus 9 Hz |
| 3. Soundpost thinned through the center | minus 8 Hz |
| 4. Wood removal from top plate and bar | minus 8 Hz |
| 5. Heavier bassbar | plus 10 Hz |
| 6. Heavier liners | plus 4 Hz |
These numbers will probably vary from instrument to instrument. For violins with an A1 delta B1 of over 75 Hz some or all of these first four methods might produce desirable results. Raising the B1 frequency using methods 5 and 6 gave more power and brighter tone to a violin with an A1-B1 delta of 40 Hz. (Hutchins and Rodgers, 1992)
Notice that all the above changes involve only the B1 mode frequency. It is not practical to try to change the frequency of the A1 mode once the dimensions (especially the length) and the stiffnesses of the violin body are established. Reducing the thickness of the top plate near the ends of the bassbar will reduce A1 frequency a few Hz, but should be done with caution.
WOOD AND WOOD PRIME TONES
It is important to know that when the violin is bowed, the strongest tone in the A1-B1 range is NOT at the A1 or the B 1 frequency, but somewhere in between depending on the relative strengths of these two modes. The effect of bowing is to combine these two strong resonances into a single strong tone labeled MAIN WOOD (W) as can be seen at the top of the chart. The MAIN WOOD frequency is usually the haunt of the wolf-tone because the stored energy in these two strong resonances is greater than the bow can handle, and the tone jumps back and forth between A1 and B1, causing a warble. In cellos the wolf-tone sometimes jumps an octave due to the near octave relation of the A0 and A1 modes in these instruments. (Schelleng 1962)
Also there is a strong bowed tone an octave below the MAIN WOOD, labeled WOOD PRIME (W') which is due to second harmonic reinforcement by the MAIN WOOD resonance. WOOD PRIME does not show on a sine wave curve, but only appears with the broadband input from the bowed string.
THE HUM TONE AS DIFFERENT FROM THE BLOW TONE
If one BLOWS across the G-side f-hole as described above, the PITCH of the A0 mode is heard. However; if one HUMS into the f-hole, a strong tone two to three semitones below the A0 is heard. This HUM tone can also be sensed by placing the thumb and fingers around each end of the body and feeling a strong vibration in these areas when the HUM tone is reached. This HUM tone is at the pitch of the WOOD prime tone, an octave below that of the MAIN WOOD resonance.
It has been found that in matching the pitch of the B0 mode to that of the HUM tone an even greater improvement in the overall sound and playing qualities sometimes results than when the B0 pitch is matched to that of the A0. In this case the match is related to the octave below two strong resonances, A1 and B1, rather than just to A0. Also it is sometimes easier, depending on the frequencies of B0 relative to either A0 or W', to match B0 to one or the other.
When the article by Deena Spear (1987) was written, we did not understand the difference between the BLOW tone and the HUM tone. Considerable research comparing bowed "loudness" curves with various single frequency tests has shown the mechanism causing the difference between the BLOW and the HUM tone as given here. Spear actually described matching the B0 mode to the HUM tone. (C.M. Hutchins, personal communication)
TAILPIECE MATCHING
Experienced violin makers are well aware that a tail-piece, when tapped sometimes gives out a strong singing vibration that seems to enhance the sound of the whole instrument. Various methods are used to achieve this condition such as tuning the string-ends between bridge and tailpiece to certain pitches, adjusting the length of the tail gut, and changing the weight of the tailpiece or tuners.
Experiments are now showing that this desirable condition is achieved when the vigorous motion of the tailpiece as a whole is matched to that of the frequency or to a sub-multiple of a strong body or cavity mode frequency. This frequency of the whole tailpiece is found between 120 and 140Hz, usually around 130 Hz. Thus far, tonal enhancement has resulted when the tailpiece frequency is matched to: (a) the B-1 mode, (b) 1/2 the frequency of the A0-B0 combination, (c) 1/2 either A0 or B0, (d) 1/2 WOOD PRIME or 1/4 MAIN WOOD frequency (which are the same). (Hutchins 1993)
THE TWO CHARTS summarize these desirable mode tunings and indicate various methods of achieving them without very expensive electronic equipment. It should be noted that HUMMING into the f-hole does NOT give the octave below the pitch of the A1 cavity mode, but rather that of WOOD PRIME (W') which is somewhat lower. A forthcoming article by Alan Carruth in this Journal will describe a relatively inexpensive setup for pressure testing for the frequencies of the A1 and B1 modes inside the cavity. This is the only test method we know so far that will give the correct relative frequencies of the A1 and B1 modes (Hutchins 1989). Measurements made off the body of the instrument or the top of the bridge may be useful, but the frequencies, particularly of the B1 mode, are altered depending on how far the measurement point or the feet of the bridge are from the nodal lines of a given mode.
The approximate relative frequencies of B-1, B0, B1 and the tailpiece can be found by soft mounting the violin horizontally at the nut and at a nodal line across the body (see chart) over your plate testing loudspeaker. Sprinkle glitter on the end of the fingerboard and the string-end of the tailpiece and sweep through the range of 100 to 1000Hz until the glitter bounces off at the approximate frequency of each of these modes. (Ekwall 1990)
There is still much to be learned about how the body and cavity modes of the violin interact to produce the wonderful sounds we hear from a fine violin in the hands of a skilled player. There are many more of these interactions at higher frequencies that are not yet understood at all. No wonder the crafting and the physical parameters of every piece of wood that goes into the construction and final adjustment of a violin can make a difference to the tonal qualities! It is a tribute to violin makers over the centuries that they have been able to cope intuitively with all these subtle variations to create such beautiful sounding instruments.
Charts
Prominent Modes of the Violin below 600Hz
Strong Bowed Tones and "Subharmonic" Tones Based on Harmonic Reinforcement
Tailpiece Mode Tuning
REFERENCES
Condax, L.W. (1988), "The soundpost of the violin," J. Catgut Acoust. Soc. Vol. 1 (Series 2) p. 28. Reprinted from Catgut Acoust. Soc. NL. No. 2, Nov. 1964.
Ekwall, A. (1990) "Tuning air-body resonances for the violin maker," Catgut Acoust. Soc. J. Vol. 1, No. 6 (Series 2) p. 37.
Hutchins, C.M. (1989), "A measurable controlling factor in the tone and playing qualities of violins," J. Catgut Acoust. Soc. Vol. 1, No. 4 (Series 2), pp. 10-15.
Ibid. (1990a) "The cavity (air) modes of the violin," J. Catgut Acoust. Soc., Vol. 1, No. 5 (Series 2), pp. 34-35.
Ibid. (1990b) "Some effects of adjusting the A0 and B0 modes of the violin to the same frequency," Ibid. pp. 35-37.
Ibid. (1990c) "Acoustical effects of "dressing down" the violin finger board and/or thinning the violin neck." Ibid. p. 37
Ibid. (1990d) "Sympathetic vibration and coupling of resonances." Catgut Acoust. Soc. J. Vol. 1, No. 6 (Series 2), pp. 40-41.
Ibid. (1993) "The effect of relating the tailpiece frequency to that of other violin modes," Catgut Acoust. Soc. J., Vol. 2, No. 3 (Series 2), pp. 5-8.
Hutchins, C.M. and Rodgers, O.E. (1992) "Methods of changing the frequency spacing (delta) between the A1 and B1 modes of the violin," Catgut Acoust. Soc. J., Vol. 2, No. 1 (Series 2) pp. 13-19.
Spear, D.Z., "Achieving an air-body coupling in violins, violas and cellos: a practical guide for the violin maker." Catgut Acoust. Soc. J. #47, pp. 4-7.